Hey guys, in my last article I told you about permutations and the difference between both permutation and combinations. In this article we are gonna learn more about Combinations and uses of these arrangements.
Link for my last article : Combinations and Permutations
Combinations
Now we noticed that in Permutation we check every small detail and everything is in order but Combinations is completely opposite to it. In Combinations we are free to choose and we have no restriction for orders too. So Combinations and Permutations are like College and School. Now you would be able understand the difference properly. After the difference comes your actual meaning of this term Combinations.
Now let us take the same example as before. But this time I am a bit kanjoos(stingy), I don't want to give three different cars but three same bikes. So how many ways are there in which i can give these 3 bikes to 9 friends?? Eventually this time the order does not matter. Giving a bike to Arya then Bhavesh and then Chirayu is same as giving a bike to Chirayu then Bhavesh and at last to Arya. It is same in any order as all of them are unhappy.
So now how many ways are there in which I can give these 3 bikes to them. In the first I have 3 options, then for the second 2 options are left and at the last only option. So the total is 3*2*1=6.
By this we could conclude that if you have "x" number of people and want to know how many possible ways are their for them then it is " x! ". You notice that these 6 ways are just useless for combinations as there is no specific order required in combinations. Now we know P(n,r) and also all the useless possibilities, so time to find combinations.
If we want to find out all the possible combinations then we just find all the permutations and divide it by all the useless possibilities. In this example we get 504 permutations ( from my last article) and we divide it by 6 useless ways and in the end we get 504/6 = 84 combinationsin all for the 9 friends.
So the Formula we get for Combinations is
C (n,r) = P(n,r) / r!
Which in the universal method can be written as
C (n,r) = n! / (n-r)! r!
Link for my last article : Combinations and Permutations
Combinations
Now we noticed that in Permutation we check every small detail and everything is in order but Combinations is completely opposite to it. In Combinations we are free to choose and we have no restriction for orders too. So Combinations and Permutations are like College and School. Now you would be able understand the difference properly. After the difference comes your actual meaning of this term Combinations.
Now let us take the same example as before. But this time I am a bit kanjoos(stingy), I don't want to give three different cars but three same bikes. So how many ways are there in which i can give these 3 bikes to 9 friends?? Eventually this time the order does not matter. Giving a bike to Arya then Bhavesh and then Chirayu is same as giving a bike to Chirayu then Bhavesh and at last to Arya. It is same in any order as all of them are unhappy.
So now how many ways are there in which I can give these 3 bikes to them. In the first I have 3 options, then for the second 2 options are left and at the last only option. So the total is 3*2*1=6.
By this we could conclude that if you have "x" number of people and want to know how many possible ways are their for them then it is " x! ". You notice that these 6 ways are just useless for combinations as there is no specific order required in combinations. Now we know P(n,r) and also all the useless possibilities, so time to find combinations.
If we want to find out all the possible combinations then we just find all the permutations and divide it by all the useless possibilities. In this example we get 504 permutations ( from my last article) and we divide it by 6 useless ways and in the end we get 504/6 = 84 combinationsin all for the 9 friends.
So the Formula we get for Combinations is
C (n,r) = P(n,r) / r!
Which in the universal method can be written as
C (n,r) = n! / (n-r)! r!
Common Life Examples for Permutation and Combination
- Combo Lock Designers :
2. Seating Arrangements :
These days managing a crowd for an large event has become simpler with the use of Combinations and
Permutations. You can now get the accurate number of possibilities rather than just confusing yourself up with some guessing game.
3. Selecting A Phone Number :
Every teen wants a phone and a phone number that he can share with everyone. And that is the time
when this concept helps. For a phone number the first four digits are fixed and you can only customize
the last 6 digits. With the help of Combinations you know the exact ways and you could find the best possible number.
I hope you guys have understood the concept of Permutation and Combinations. If the article was interesting and you loved it then do share it with your friends, family, teachers,neighbors and everyone.
If you want any other math topic to be published then do write it in the comments section,. Thanks for reading this article and spending your valuable time with us.
You may also like these articles from High School Pedia :

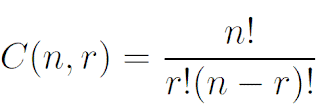



Comments
Post a Comment